ベータ崩壊

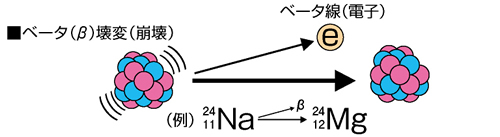
ベータ崩壊（ベータほうかい、beta decay）とは、原子核の放射性崩壊のうち、ベータ粒子（電子または陽電子）の放出をともなうものをいう。ベータ壊変（ベータかいへん）ともいう。

本記事では主に原子核中の中性子が陽子へ変化するベータ崩壊について述べる。これは「中性子 ⇄ 陽子＋電子＋反電子ニュートリノ」の遷移過程の右方向への遷移である。逆方向への遷移は電子捕獲（逆ベータ崩壊）と呼ばれる。

概要

中性子のベータ崩壊においては、原子核中の中性子が崩壊し電子と反電子ニュートリノを放出すると同時に陽子が残る。中性子が陽子に変化すると解釈してもよい。このとき放出される電子はベータ線（β線）の一種である。原子は質量数を維持し原子番号の一つ大きい元素へ変わる。

より広義には、ベータ粒子(電子)と反電子ニュートリノを放出するβ⁻崩壊（負のβ崩壊、陰電子崩壊）、陽電子と電子ニュートリノを放出するβ 崩壊（正のβ崩壊、陽電子崩壊）、軌道電子を原子核に取り込み電子ニュートリノを放出する電子捕獲、二重ベータ崩壊、二重電子捕獲 (double electron capture) を合わせてベータ崩壊と呼ぶ。

いずれの崩壊においても、原子の質量数は変化しない。つまりベータ崩壊は原子が同重体へ推移する現象である。

ベータ崩壊の理論

放射性物質の放つ放射線は、ヘリウム原子核であるアルファ線（α線）、電子であるベータ線（β線）、波長の非常に短い電磁波であるガンマ線（γ線）からなる。ところで、アルファ線とガンマ線のエネルギー分布は常に離散的な値を示すが、ベータ線だけはなぜかそのエネルギー分布は連続的な値を示す。この不可解なベータ線の連続的なエネルギーレベルを説明するためにベータ崩壊の理論が探索された。

まず、ベータ崩壊をする原子核は量子力学における状態として連続的な状態を取ると考えられたが、ベータ崩壊をする原子核の放出するアルファ線やガンマ線はやはり離散的なものであったことから否定された。次に、はじめはアルファ線やガンマ線と同一のエネルギーレベルで放出されたベータ線が、二次的に散乱されたり、吸収されるため連続的な値を取るのではないかと予想されたが、Ellis と Wooster によって否定された（1927年）。

ヴォルフガング・パウリは、新粒子の存在を仮定すればベータ崩壊の連続エネルギー分布が説明できることを指摘した。すなわち、ベータ崩壊においては電子と一緒に、何か普通の方法では観測できない未知の粒子がもう一つ放出されており、ベータ崩壊の前後における原子核のエネルギーの差は、電子とこの新粒子との間に分けられているため、ベータ線（電子）のエネルギーは0からある一定値までの連続的な任意の値を取るのではないかとした（1931年）。

これに対して、ニールス・ボーアは1934年に、ベータ崩壊のような原子核の内部の現象は原子スペクトルなどとは違って、もっと程度の高い本質的に新しい物理学の範囲に属するから、必ずしもエネルギー保存則は厳密にも成り立たなくても良いという仮説を提出し、パウリの新粒子説に反対した（エネルギー非保存仮説）。しかしながら、その後このボーアのエネルギー非保存仮説は、実験及び理論の両面からその矛盾が指摘され、結局パウリの新粒子説が優勢となった。そのパウリの新粒子はニュートリノ（neutrino；中性微子）と名付けられ、ベータ崩壊の理論（弱い相互作用の理論）建設の端緒となった。

エネルギー保存則の観点から見ると、β 崩壊および電子捕獲は陽子の静止質量（938.27 MeV）が中性子の静止質量（939.57 MeV）よりも小さいため、真空中では本来発生し得ない事象である。この陽子と中性子の静止質量差よりも、崩壊前後の結合エネルギーの差が大きい（Q値が正である）核種のみ、これらの反応が起こりえる。

ベータ崩壊の各モード

各種ベータ崩壊のメカニズムを記す。

ここでは電子を ${\displaystyle {\ce {{\mathit {e}}^{-}}}}$、陽電子を ${\displaystyle {\ce {{\mathit {e}}^{ }\,}}}$、陽子を ${\displaystyle \mathrm {p} \,}$、中性子を ${\displaystyle {\mathit {n}}\,}$、電子ニュートリノを ${\displaystyle \nu _{\mathrm {e} }\,}$、アップクォークを ${\displaystyle \mathrm {u} \,}$、ダウンクォークを ${\displaystyle \mathrm {d} \,}$、負電荷を持つWボソンを ${\displaystyle \mathrm {W} ^{-}\,}$ と表記する。なお、反粒子は（例えば ${\displaystyle {\bar {\nu }}_{\mathrm {e} }}$ のように）アッパーバーであらわす。

β⁻崩壊

中性子が電子（ベータ粒子）と反電子ニュートリノを放出して陽子になる現象。単にベータ崩壊といった場合これを指す。一般的に、中性子過剰核、すなわち安定同位体よりも中性子の多い核種でβ⁻崩壊が発生する。

${\displaystyle {\ce {{\mathit {n}}->p^{ }\ {\mathit {e}}^{-}\ {\bar {\nu }}_{\mathit {e}}}}}$

クォークのレベル（右図参照）では、中性子のダウンクォークがアップクォークに変化する。次のように表される。

${\displaystyle \mathrm {d} ^{(1/3)-}\to \mathrm {u} ^{(2/3) } {\mathit {e}}^{-} {\bar {\nu }}_{\mathit {e}}}$

原子核内で起こった場合、原子番号が1つ大きい元素に変化する。

${\displaystyle {\ce {_{18}^{42}Ar -> _{19}^{42}K}}}$、アルゴン42からカリウム42（半減期 32.9年）。

β 崩壊

陽子が陽電子（ベータ粒子）と電子ニュートリノを放出して中性子になる現象。正のβ崩壊、陽電子崩壊とも呼ぶ。一般的に陽子過剰核、すなわち安定同位体よりも中性子の少ない核種でβ 崩壊が発生する。

${\displaystyle {\ce {p^{ }->{\mathit {n}}\ {\mathit {e}}^{ }\ \nu _{\mathit {e}}}}}$

クォークのレベルでは、陽子のアップクォーク一個がダウンクォークに変化する。次のように表される。

${\displaystyle \mathrm {u} ^{(2/3) }\to \mathrm {d} ^{(1/3)-} {\mathit {e}}^{ } \nu _{\mathit {e}}}$

原子核内で起こった場合、原子番号が一つ小さい元素に変化する。

${\displaystyle {\ce {_{60}^{132}Nd -> _{59}^{132}Pr}}}$、ネオジム132からプラセオジム132（半減期 1.75分）。

電子捕獲

陽子が軌道上の電子を捕獲して中性子に換わり、電子ニュートリノと特性X線を放つ現象。ベータ粒子は放出しない。ε または EC (electron capture) と略される。書籍によって「軌道電子捕獲」と記述されることもある。

${\displaystyle {\ce {p^{ }{} {\mathit {e}}^{-}->{\mathit {n}}{} \nu _{\mathit {e}}}}}$

原子番号が一つ小さい元素に変化する。崩壊のメカニズムは大きく異なるものの、原子番号が一つ小さい同重体となる結果だけを見れば、β 崩壊と電子捕獲は同じものといえる。

${\displaystyle {\ce {_{18}^{37}Ar -> _{17}^{37}Cl}}}$、アルゴン37から塩素37（半減期 36日）

二重ベータ崩壊

ベータ崩壊が、ほぼ同時に二回起きる現象。一回のベータ崩壊が原子核の質量が増える変化であるため起こらず、ベータ崩壊が二回起きると質量が減る原子核に起きる。非常にまれにしか起きない現象であるため、半減期は非常に長い。

ニュートリノを放出する場合

単に、通常のβ⁻崩壊などが二重に起きる。

ニュートリノを放出しない場合

ニュートリノが粒子と反粒子が同じであるマヨラナ粒子である場合などに起きる現象。標準理論では起きない現象であり、2006年現在未検証である。この崩壊を観測することにより、ニュートリノの質量やスピンについての不明な点が解明できる可能性があるため、研究が進められている。なお、前述のマヨラナ粒子が関係するもの以外に、超対称性などが関係して起きる可能性も示されている。

ニュートリノがマヨラナ粒子である場合、例えば次のように二重ベータ崩壊が起きる可能性がある。

${\displaystyle {\ce {{\mathit {n}}->p^{ }{} {\mathit {e}}^{-}{} {\bar {\nu }}_{\mathit {e}}}}}$（1つ目のベータ崩壊）

${\displaystyle {\ce {{\bar {\nu }}_{\mathit {e}}->\nu _{\mathit {e}}?}}}$（反電子ニュートリノと電子ニュートリノは同一？）

${\displaystyle {\ce {{\mathit {n}} \nu _{\mathit {e}}->p^{ }{} {\mathit {e}}^{-}}}}$（2つ目のベータ崩壊）

結局、全体では次のようになるので、ニュートリノは放出されない。

${\displaystyle {\ce {2{\mathit {n}}->2p^{ }{} 2{\mathit {e}}^{-}}}}$

二重電子捕獲

複数の崩壊モードを持つ核種

核種によっては二つ以上の崩壊モードを持つものがあり、特有の確率でいずれかのモードで崩壊する。一般的に陽子数と中性子数が共に偶数のほうが安定であり、そのように安定な娘核種が複数存在する場合にそのようなことが起こりやすい。ここに記載した例はすべて親核種の陽子数（すなわち原子番号）が奇数のものである。

β⁻崩壊と電子捕獲

塩素36（半減期 30万1000年）

${\displaystyle {}_{17}^{36}\mathrm {Cl} \,{\overset {\beta ^{-}}{\longrightarrow }}\,{}_{18}^{36}\mathrm {Ar} }$

${\displaystyle {}_{17}^{36}\mathrm {Cl} \,{\overset {\varepsilon }{\longrightarrow }}\,{}_{16}^{36}\mathrm {S} }$

イリジウム192（半減期 73.83日）

${\displaystyle {}_{\ 77}^{192}\mathrm {Ir} \,{\overset {\beta ^{-}}{\longrightarrow }}\,{}_{\ 78}^{192}\mathrm {Pt} }$

${\displaystyle {}_{\ 77}^{192}\mathrm {Ir} \,{\overset {\varepsilon }{\longrightarrow }}\,{}_{\ 76}^{192}\mathrm {Os} }$

β 崩壊と電子捕獲

アルミニウム26（半減期 71万7000年）

${\displaystyle {}_{13}^{26}\mathrm {Al} \,{\overset {\beta ^{ }}{\longrightarrow }}\,{}_{12}^{26}\mathrm {Mg} }$

${\displaystyle {}_{13}^{26}\mathrm {Al} \,{\overset {\varepsilon }{\longrightarrow }}\,{}_{12}^{26}\mathrm {Mg} }$

マンガン52（半減期 5.59日）

${\displaystyle {}_{25}^{52}\mathrm {Mn} \,{\overset {\beta ^{ }}{\longrightarrow }}\,{}_{24}^{52}\mathrm {Cr} }$

${\displaystyle {}_{25}^{52}\mathrm {Mn} \,{\overset {\varepsilon }{\longrightarrow }}\,{}_{24}^{52}\mathrm {Cr} }$

β⁻崩壊とβ 崩壊と電子捕獲

カリウム40（半減期 12億7700万年）

${\displaystyle {}_{19}^{40}\mathrm {K} \,{\overset {\beta ^{-}}{\longrightarrow }}\,{}_{20}^{40}\mathrm {Ca} }$

${\displaystyle {}_{19}^{40}\mathrm {K} \,{\overset {\beta ^{ }}{\longrightarrow }}\,{}_{18}^{40}\mathrm {Ar} }$

${\displaystyle {}_{19}^{40}\mathrm {K} \,{\overset {\varepsilon }{\longrightarrow }}\,{}_{18}^{40}\mathrm {Ar} }$

ヨウ素126（半減期 13日）

${\displaystyle {}_{\ 53}^{126}\mathrm {I} \,{\overset {\beta ^{-}}{\longrightarrow }}\,{}_{\ 54}^{126}\mathrm {Xe} }$

${\displaystyle {}_{\ 53}^{126}\mathrm {I} \,{\overset {\beta ^{ }}{\longrightarrow }}\,{}_{\ 52}^{126}\mathrm {Te} }$

${\displaystyle {}_{\ 53}^{126}\mathrm {I} \,{\overset {\varepsilon }{\longrightarrow }}\,{}_{\ 52}^{126}\mathrm {Te} }$

α崩壊とβ⁻崩壊

ビスマス210（半減期 5.013日）

${\displaystyle {}_{\ 83}^{210}\mathrm {Bi} \,{\overset {\alpha }{\longrightarrow }}\,{}_{\ 81}^{206}\mathrm {Tl} }$

${\displaystyle {}_{\ 83}^{210}\mathrm {Bi} \,{\overset {\beta ^{-}}{\longrightarrow }}\,{}_{\ 84}^{210}\mathrm {Po} }$

アクチニウム227（半減期 21.77年）

${\displaystyle {}_{\ 89}^{227}\mathrm {Ac} \,{\overset {\alpha }{\longrightarrow }}\,{}_{\ 87}^{223}\mathrm {Fr} }$

${\displaystyle {}_{\ 89}^{227}\mathrm {Ac} \,{\overset {\beta ^{-}}{\longrightarrow }}\,{}_{\ 90}^{227}\mathrm {Th} }$

ベータ崩壊による壊変系列

ベータ崩壊後の原子核が不安定な場合、さらに崩壊を行うことになり、数種の同重体を経由する壊変系列を形成する。特に核分裂によって生じた核分裂生成物は、陽子数と中性子数との均衡を欠いており、両者の均衡を保てるところ（ベータ安定線）までベータ崩壊を繰り返す。r過程は魔法数を持った中性子過剰核が同様のことを起こすことで核種分布の山を作るという仮説により推定されている。

酸素20からフッ素20、さらにネオン20。

${\displaystyle {}_{\ 8}^{20}\mathrm {O} \,{\overset {\beta ^{-}}{\longrightarrow }}\,{}_{\ 9}^{20}\mathrm {F} \,{\overset {\beta ^{-}}{\longrightarrow }}\,{}_{10}^{20}\mathrm {Ne} }$

脚注

参考文献

• エンリコ・フェルミ 著、小林稔 編『原子核物理学』吉岡書店〈物理学叢書 ; 第1〉、1954年。全国書誌番号:56015532。 
• 武谷 三男, 豊田 利幸, 中村 誠太郎『現代物理学（原子核）』 第八巻、岩波書店〈岩波講座〉、1959年。 
• 富永健、佐野博敏『放射化学概論』（第4版）東京大学出版会、2018年。ISBN 978-4-13-062512-8。 

関連項目